Table of Contents
Definisi dan Konsep Dasar Surjektif
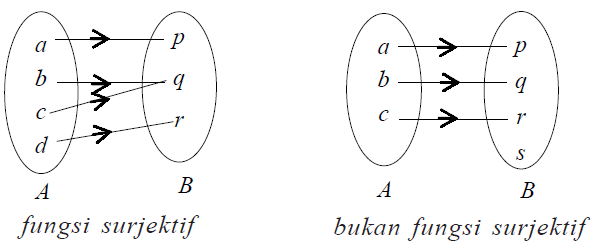
Fungsi surjektif atau fungsi onto merupakan salah satu konsep penting dalam matematika. Fungsi ini memiliki sifat yang menarik, di mana setiap elemen dalam kodomain memiliki pasangan dengan setidaknya satu elemen dalam domain. Dalam fungsi surjektif, range atau daerah hasilnya sama dengan kodomainnya. Dalam matematika, fungsi surjektif dituliskan sebagai f(x) = y, di mana untuk setiap y dalam kodomain, ada setidaknya satu x dalam domain yang memenuhi persamaan tersebut. Fungsi surjektif memiliki peran penting dalam pemetaan relasi fungsi, di mana semua elemen dalam kodomain berelasi dengan elemen dalam domain. Dengan memahami konsep ini, kita dapat memahami lebih dalam tentang hubungan antara himpunan dan fungsi dalam matematika.
Sifat-sifat Fungsi Surjektif
Fungsi surjektif memiliki beberapa sifat yang dapat dijelaskan secara spesifik. Berikut adalah penjelasan mengenai sifat-sifatnya, yaitu sebagai berikut:
1. Range sama dengan kodomain: Fungsi ini memiliki sifat bahwa daerah hasilnya (range) sama dengan kodomainnya. Artinya, setiap elemen dari kodomain memiliki relasi dengan setidaknya satu elemen dari domain. Tidak ada elemen di kodomain yang tidak memiliki pasangan di domain.
2. Setiap elemen di kodomain memiliki pasangan di domain: Dalam fungsi surjektif, setiap elemen di kodomain memiliki setidaknya satu pasangan di domain. Dengan kata lain, untuk setiap elemen y di kodomain, terdapat setidaknya satu elemen x di domain sehingga f(x) = y.
3. Tidak ada elemen di kodomain yang tertinggal: Fungsi ini memastikan bahwa tidak ada elemen di kodomain yang tidak memiliki pasangan di domain. Artinya, setiap elemen di kodomain terhubung dengan setidaknya satu elemen di domain.
Secara matematis, sifat-sifat tersebut dapat dituliskan sebagai berikut:
- Range fungsi surjektif: f(a) = b, di mana a adalah elemen di domain dan b adalah elemen di kodomain.
- Untuk setiap elemen y di kodomain, terdapat setidaknya satu elemen x di domain sehingga f(x) = y.
- Tidak ada elemen di kodomain yang tidak memiliki pasangan di domain.
Dengan demikian, fungsi surjektif merupakan fungsi yang memastikan bahwa setiap elemen di kodomain terhubung dengan setidaknya satu elemen di domain, dan tidak ada elemen di kodomain yang tertinggal.
Contoh Penerapan Fungsi Surjektif
Fungsi surjektif adalah fungsi yang memiliki range (daerah hasil) yang sama dengan kodomainnya. Artinya, setiap elemen dari kodomain memiliki pasangan atau relasi dengan setidaknya satu elemen dari domain.
Contoh penerapan fungsi surjektif dapat ditemukan dalam berbagai bidang, seperti matematika, ilmu komputer, dan ekonomi, yaitu sebagai berikut:
1. Matematika
Misalkan terdapat fungsi f: A → B, dengan A = {1, 2, 3} dan B = {4, 5, 6}. Fungsi ini dapat didefinisikan sebagai f(x) = x + 3. Dalam hal ini, setiap elemen dari B memiliki pasangan dengan elemen dari A. Misalnya, f(1) = 4, f(2) = 5, dan f(3) = 6. Dengan demikian, fungsi ini merupakan fungsi surjektif.
2. Ilmu Komputer
Dalam pemrograman, fungsi surjektif dapat digunakan untuk memetakan data dari satu himpunan ke himpunan lain. Misalnya, terdapat fungsi yang mengonversi suhu dari Celsius ke Fahrenheit. Setiap nilai Fahrenheit memiliki pasangan dengan setidaknya satu nilai Celsius. Dalam hal ini, fungsi ini merupakan fungsi surjektif.
3. Ekonomi
Dalam ekonomi, fungsi surjektif dapat digunakan untuk menggambarkan hubungan antara permintaan dan penawaran suatu produk. Misalnya, terdapat fungsi yang menggambarkan hubungan antara harga suatu produk dan jumlah produk yang dibeli oleh konsumen. Setiap harga memiliki pasangan dengan setidaknya satu jumlah produk yang dibeli. Dalam hal ini, fungsi ini merupakan fungsi surjektif.
Dalam semua contoh di atas, fungsi surjektif memastikan bahwa tidak ada elemen di kodomain yang tidak memiliki pasangan dengan elemen di domain. Hal ini memungkinkan setiap elemen di kodomain dapat dicapai atau direpresentasikan oleh setidaknya satu elemen di domain.
Keindahan dalam Kemungkinan Tak Terbatas
Dalam matematika, konsep keindahan sering kali terkait dengan kemungkinan tak terbatas. Kemungkinan tak terbatas mengacu pada fakta bahwa dalam matematika, kita dapat mengeksplorasi dan memahami konsep-konsep yang tidak memiliki batasan atau pembatasan tertentu. Hal ini memberikan ruang bagi kreativitas dan eksplorasi yang tak terbatas, yang pada gilirannya menghasilkan keindahan dalam matematika.
Salah satu contoh keindahan dalam kemungkinan tak terbatas adalah dalam teori himpunan. Teori himpunan mempelajari konsep dasar tentang himpunan, elemen, dan hubungan antara himpunan. Dalam teori himpunan, kita dapat membangun himpunan yang tak terbatas, seperti himpunan bilangan bulat atau himpunan bilangan real. Kemungkinan tak terbatas ini memberikan keindahan dalam memahami dan menjelajahi struktur matematika yang kompleks.
Selain itu, dalam analisis matematika, kita juga dapat menemukan keindahan dalam kemungkinan tak terbatas. Analisis matematika mempelajari konsep-konsep seperti limit, turunan, dan integral. Dalam analisis matematika, kita dapat memperluas pemahaman kita tentang fungsi dan menggali lebih dalam tentang sifat-sifatnya. Kemungkinan tak terbatas dalam analisis matematika memungkinkan kita untuk mengeksplorasi berbagai fungsi yang tak terbatas, seperti fungsi eksponensial atau fungsi trigonometri. Keindahan terletak pada pemahaman yang mendalam tentang fungsi-fungsi ini dan bagaimana mereka berinteraksi satu sama lain.
Dalam matematika, keindahan sering kali terkait dengan kemungkinan tak terbatas. Kemungkinan tak terbatas memberikan ruang bagi eksplorasi dan kreativitas yang tak terbatas, yang menghasilkan keindahan dalam matematika. Dalam teori himpunan, kita dapat membangun himpunan yang tak terbatas, sementara dalam analisis matematika, kita dapat mengeksplorasi fungsi-fungsi yang tak terbatas. Keindahan terletak pada pemahaman yang mendalam tentang konsep-konsep ini dan bagaimana mereka berinteraksi satu sama lain. Dengan memahami dan menghargai kemungkinan tak terbatas dalam matematika, kita dapat melihat keindahan yang tersembunyi di baliknya.